It considers the function f: R — R >, f (x) = p x + q, where p
and q are real numbers.
a) find the real numbers p and q knowing that
f (1) = 1 and
f (2) =-1
b) for p = -2 and q = 3, graph the function using
xOy coordinates system.
Solution:
The function f (x) = p x + q, is a function of the first degree
(because power of unknown x is equal to 1 (a linear function).
Hypotesis conditions shows us that when the unknown x takes the
value of 1 (or if we substitute x with 1) the value of the function (f) is 1
and when x takes the value 2 the value of function (f) is -1. We write as
follows:
f (1) = 1 ; 1 = p ∙
1 + q
f (2) = -1 ; -1 = p ∙ 2 + q ;
these two relations must be valid simultaneously (at the same
time) because the text put an "and" between them. This ' and ' show
us that we have to solve the equations as a system of two lineaar equations and
two unknowns.
Solving the system we obtain the p and q values required by the
problem.
B) The function is:
f(x) = -2 x +3
To graph the function we need two points. Since the graph of function of the first
degree is a straight line, and we know that a straight line can be drawn if we
know at least two points on the line, we use the so-called x-intercept and
y-intercept (the places where the graph
hits the coordinates axis ox and oy, respectively).
A coordinate system specifies each point
uniquely in a plane by a pair of numerical coordinates, which are the signed
distances to the point from two fixed perpendicular directed lines, measured in
the same unit of length. Each reference line is called a coordinate axis
or just axis of the system, and the point where they meet is its origin,
usually at ordered pair O (0, 0). The coordinates can also be defined as the
positions of the perpendicular projections of the point onto the two axis,
expressed as signed distances from the origin.
The point M has the coordinates (xM, yM) we read: the point M of
coordinates xM and yM). The distance from a point M to the axis Oy
is called the abscissa of point (or the x-coordinate of the point) i.e., xM. The distance from a point to the axis Ox
is called ordinate (or y-coordinate of the point) that is, yM. The coordinate axis Ox is called abscissa
and all points that belong to this straight have coordinates (xM, 0) ... the
letter M is taken just for example ... The coordinate axis Oy is called the
"ordinate" and all points that belong to this straight are (0, yM)
When the graph of function intersects the axis Oy we find a point A
which belongs to and the graph function, so this point, noted for example the
letter A has x-coordinate equal to 0 . Which means that we replace in the
function the value of xA with 0 we get coordinated point of yA.
xA =
0 => yA = f(xA) = f(0) = -2 ∙ 0 + 3
= 3.
A ( 0 ; 3)
When the graph intercepts Ox we find a point with the ordinate
equal to 0.
So at this point, for example with the letter B is the
y-coordinate is equal to 0. Which means that we replace function on expression
yB by 0 we achieve the xB value. .
yB =
0 => yB = f(xB) = -2 ∙ xB + 3 = 0 => -2 ∙ xB = - 3 => xB = 3/2
B ( 3/2 ; 0)
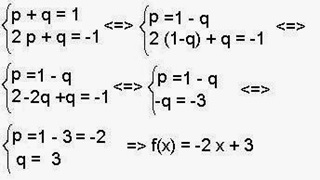

Niciun comentariu:
Trimiteți un comentariu